Stefan-Boltzmann's law relates the integral of the spectral hemispherical density of the radiant flux with the temperature of isothermal black surface. Proceeding from the quantum theory of radiation transfer it has been shown that the spectral and hemispherical density of the radiant flux from the isothermal black surface in vacuum is expressed by Planck's formula

where iλb is the radiation intensity of the black body (Planck's function), T is the absolute temperature, the constants C1 = 0.59544 · 10−16 Wm2, C2 = 1.4388 · 10−2 mK, C1 = 2h
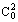 and C2 = hC0/ k, where C0 is the velocity of light in vacuum, h = 6.6262 · 10−34 Js is Planck's constant, and k = 1.3806 · 10−23 J/K is Boltzmann's constant.
and C2 = hC0/ k, where C0 is the velocity of light in vacuum, h = 6.6262 · 10−34 Js is Planck's constant, and k = 1.3806 · 10−23 J/K is Boltzmann's constant.
In Equation 1 radiant flux eλb and the radiation intensity ilb are related by
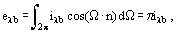
where dΩ = sin θ dθ d
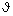 is the element of a solid angle along Ω, n the direction of a normal to the surface element. The maximum value of Planck's function is achieved at λmax T = C3 = 2.8978 · 10−3 mK (Wien's displacement law).
is the element of a solid angle along Ω, n the direction of a normal to the surface element. The maximum value of Planck's function is achieved at λmax T = C3 = 2.8978 · 10−3 mK (Wien's displacement law).
Depending on the frequency ν = C0/λ or the wave number ω = 1/λ the radiation intensity of the black body in a unit interval ν or ω is

Moreover, the balance relations
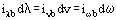
are retained.
The hemispherical surface intensity of radiant flux integrated over the entire spectrum (Stefan-Boltzmann's law) is equal to

where σ is Stefan-Boltzmann's constant (
 ).
).
The tables, as a rule, present the values of a fraction of hemispherical density of the radiant flux transferred in the wavelength interval from 0 to λ

determined as a function of the variable λT. Then the fraction of the density of the radiant flux in an arbitrary interval [λ1, λ2] is determined as

If the surface element is in a medium other than vacuum and this medium has the refractive index n, Planck's function per unit interval of wavelengths in vacuum takes the form

and Wien's and Stefan-Boilzmann's laws take the form

where λmax,n is the wavelength in a given medium.
The radiation heat flux from an isothermal nonblack surface in vacuum is calculated by the formula
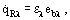
where ελ = ελ(T) is the hemispherical emissivity of the black surface made of a given material.