The trapezoidal rule is an approximate method of estimating a definite integral
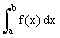 .
.
The interval of integration is separated into n partial subintervals xi, xi=1, i = 0, 1, ..., n – 1. On each subinterval a subintegral function is replaced by a linear one.
An integral on the interval xi, xi+1 is calculated approximately by the formula for the trapezoid area
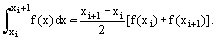
The summation of the left and the right parts of this approximate equality brings about the trapezoidal rule

For the case of n equidistant cusps the expression is simplified and is reduced to the form

This quadrature formula is correct for trigonometric functions
 ,
,
 , k = 0, 1, ..., n – 1. When b – a = 2π, the trapezoidal formula is exact for all trigonometric polynomials of order not higher (n – 1).
, k = 0, 1, ..., n – 1. When b – a = 2π, the trapezoidal formula is exact for all trigonometric polynomials of order not higher (n – 1).
The error of a quadrature formula |R(f)| is the modulus of the difference between the exact value of the integral and the quadrature sum, for double differentiable subintegral functions, this does not exceed

On finding a complete limit error of a quadrature formula an error of addition must also be accounted, if an addend f(xi) is calculated with an absolute error not exceeding ε, then the total error
 of the quadrature formula without considering a concluding round off error does not exceed
of the quadrature formula without considering a concluding round off error does not exceed
 ≤ (b – a)ε + |R(f)|.
≤ (b – a)ε + |R(f)|.