Radiative Transfer in Multidimensional Problems: a Combined Computational Model
Following from: Radiation of isothermal volumes of scattering medium: An error of the diffusion model; Finite-element method for radiation diffusion in nonisothermal and nonhomogeneous media
Leading to: Thermal radiation of two-phase exhaust jet
Radiative transfer in multidimensional problems is often characterized by complex angular distribution of radiative intensity. Simple differential methods for solving the radiative transfer equation (RTE), such as the diffusion approximation, which is widely used in one-dimensional problems, can be incapable of accurately predicting the radiation field in real applications, especially for media characterized by strong spatial variation of radiative properties and large temperature gradients. At the same time, even for the most complicated cases, the field of the radiation energy density obtained by using the diffusion approximation can be successfully used as an initial guess in multistep solution methods.
The angular dependence of the spectral radiation intensity is approximated too crudely by the use of simple differential methods. For example, the linear dependence of Iλ on the cosine of the angle measured from the radiation flux direction is assumed in P1 approximation. In the case of nonisothermal disperse systems with strong spatial variation of the medium radiative properties, the angular structure of the radiation field may be very complex. Therefore, high-order approximations of the spherical harmonics method would be adequate for these problems, but their application considerably increases the mathematical complexity (Ou and Liou, 1982). On the other hand, the RTE solution methods that ignore radiation scattering can lead to physically incorrect results, since the role of scattering, particularly at small angles to the boundary of a radiating volume, is usually significant even for small optical thickness of a disperse medium.
Edwards and Bobcôo (1967) and Bobcôo (1967) have proposed an iteration method employing the diffusion approximation as an initial approach for isotropic scattering media. In the case of isotropic scattering, the spectral radiation source function on the right-hand side of the RTE is isotropic:

|
(1) |
Therefore, it is reasonable to first obtain the spectral radiation energy density Iλ0(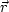 ) by using the diffusion approximation and then to solve the RTE with the known source function Fλ(
) by using the diffusion approximation and then to solve the RTE with the known source function Fλ(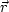 ). This idea can also be realized in the case of anisotropic scattering when the transport approximation for the scattering phase function is employed. Indeed, the RTE in the transport approximation is similar to the RTE for isotropic scattering:
). This idea can also be realized in the case of anisotropic scattering when the transport approximation for the scattering phase function is employed. Indeed, the RTE in the transport approximation is similar to the RTE for isotropic scattering:

|
(2) |
and the diffusion approximation, as before, can be easily applied to the first stage of the iterative solution procedure. This approach was used by Adzerikho et al. (1979) to model radiative transfer in a cylindrical and anisotropic scattering medium of finite height. Dombrovsky and Barkova (1986) employed the finite-element method (FEM) at the first stage of the solution procedure and developed an algorithm applicable to media of complex geometry with highly nonuniform properties. The following two-step combined method was suggested. In the first step, the variational problem for the functional
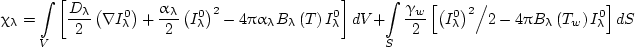
|
(3) |
is solved in the medium volume and the spectral radiation energy density Iλ0(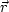 ) in the nodal points of the finite-element mesh is computed. The spectral radiative energy density Iλ0 is obtained at any point in the volume by using the linear interpolation:
) in the nodal points of the finite-element mesh is computed. The spectral radiative energy density Iλ0 is obtained at any point in the volume by using the linear interpolation:

|
(4) |
(for more details, see the article Finite-element method for radiation diffusion in nonisothermal and nonhomogeneous media). The spectral radiation intensity Iλ(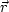 ,
,  ) is computed in the second step of the method by direct integration of the RTE. This procedure can be easily applied to a medium without external irradiation at the boundary s = 0. The formal solution along the direction
) is computed in the second step of the method by direct integration of the RTE. This procedure can be easily applied to a medium without external irradiation at the boundary s = 0. The formal solution along the direction  is
is
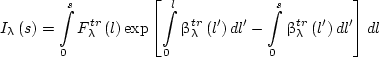
|
(5) |
The error of the combined method is influenced by the transport approximation, but the number of iterations for obtaining high-accuracy results is generally unknown. The accuracy of the combined method for selected model problems is analyzed below.
Model Problems for Thermal Radiation
First, consider the traditional model problem--the radiation of a plane-parallel layer of a homogeneous isothermal medium. For a nonscattering medium, only the second step of the combined method is necessary and the exact solution for the spectral radiative intensity at the layer surface is
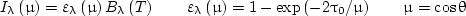
|
(6) |
where ελ is the directional emissivity of the medium layer, τ0 = αλd/2 is the spectral optical thickness of the medium layer of thickness d, and θ is the angle measured from the external normal to the layer surface. The spectral directional emissivity ελ obtained by using Eq. (6) can be compared to that obtained by using the P1 approximation:
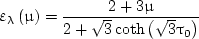
|
(7) |
Figure 1 indicates that the angular intensity distribution in the P1 approximation is physically incorrect. The combined method enables us to eliminate this effect. The latter statement is illustrated in Fig. 2 and Table 1 for a scattering medium with the transport scattering albedo ωtr = 0.5. Two computational procedures are employed at the first step of the combined method: (A) the P1 analytical solution and (N) the P1 numerical FEM solution for the layer of width w = 4.25d. In the latter case, the radiation energy density at the central line of the layer surface is determined. The reference numerical results are obtained by using a double-Gaussian quadrature of high order described in the article Radiation of an isothermal plane-parallel layer.

Figure 1. Directional emissivity of plane-parallel layer of a nonscattering medium: I - exact solution, II - P1 approximation; 1 - τ0 = 0.2, 2 - τ0 = 0.5, 3 - τ0 = 1.

Figure 2. Directional emissivity of plane-parallel layer of scattering medium at ωtr = 0.5: I - exact solution, II - combined method, variant A; 1 - τtr0 = 0.2, 2 - 0.5, 3 - 1, and 4 - 2.
Table 1. Directional emissivity of plane-parallel layer of scattering medium at τtr0 = 1 and ωtr = 0.5
| θ | ελ | ||
| Combined method | Exact solution | ||
| Variant A | Variant N | ||
| 20° | 0.6963 | 0.6959 | 0.7103 |
| 40° | 0.7298 | 0.7292 | 0.7443 |
| 60° | 0.7648 | 0.7640 | 0.7785 |
| 80° | 0.7450 | 0.7364 | 0.7540 |
One can see excellent agreement between the results of the combined method and the exact solution. The single iteration based on the radiation energy density determined by the P1 approximation at the first step appears sufficient to correctly predict the angular intensity distribution. Table 1 indicates that additional computational error of the FEM solution (variant N) is negligible (less than 1%). In contrast to the case of a nonscattering medium, the angular intensity distribution is nonmonotonic due to the increasing contribution of the radiation energy density to the source function Fλtr with the optical thickness of the medium. It goes without saying that the radiation flux is also determined with an appreciably higher accuracy due to the second step of the combined method. Even at θ = 80o, the hemispherical emissivity for variant A is equal to 0.7364 compared with the exact value of 0.745 and a value of 0.814 in the P1 approximation.
The transport approximation forms the basis of the combined method. In one-dimensional problems, the transport approximation error is small (see the article, Radiation of isothermal plane-parallel layer). Obviously, this does not mean that such small errors will be obtained in two-dimensional problems (particularly for nonisothermal volumes of nonuniform media), because the error of the transport approximation depends on the specifics of the radiative transfer problem. Nevertheless, the error of the transport approximation assessed by using the Monte Carlo (MC) method as applied to radiation of a scattering medium in a cylindrical volume of finite height is acceptable in some special cases, even for the directional intensity distribution (Dombrovsky et al., 1991). Following the paper by Dombrovsky et al. (1991), we consider two model problems involving radiative transfer in a cylindrical volume of a homogeneous and isothermal absorbing and scattering medium as described below. The choice of the model problems is motivated by engineering applications concerned with both near-field thermal effects and remote sensing of thermal radiation of two-phase jets containing highly scattered micrometer-size particles of alumina (Laredo and Netzer, 1993; Surzhikov, 2004). In contrast to the real jets, the model problems assume uniform radiative properties. However, the selected values of the radial optical thickness τtrR = 5, the scattering albedo ωtr = 0.95, and the asymmetry factor of scattering μ ≥ 0.5are close to those encountered in real problems. The length-to-radius ratio of the cylindrical volume is assumed to be equal to L/R = 4. The results presented below are obtained by using the collision-based MC method (Farmer and Howell, 1998) in the second step of the combined method, as described in a recent paper by Dombrovsky and Lipiński (2010). For each problem, the distribution of the dimensionless radiative flux leaving the cylindrical volume is computed as

|
(8) |
where q(μ) is the radiative flux intercepted by a large black and cold sphere of radius Rsph >> L, with its center coincident with the center of the cylindrical volume, μ = cosθ, where θ is the polar angle measured from the axis of the cylindrical volume.
The following methods are employed: (1) the combined method incorporating the P1 approximation, FEM and the transport approximation in the first step to obtain the radiation source function, and MC to compute the radiative flux in the second step; (2) the Monte Carlo method (referred to further as “transport MC”), incorporating the transport approximation, and (3) the reference MC method, providing the complete radiative transfer solution in a single step and using the Henyey-Greenstein scattering phase function (Modest, 2003).
Problem 1. - The thermal radiation of the medium is considered and no radiation sources at boundaries are present. The numerical results for this symmetric problem are presented in Fig. 3. One can see that the combined method agrees very well with both the transport MC method and the reference method. It is interesting that the variation of the radiation flux with the asymmetry factor of scattering is negligible. Besides the small error of the transport approximation, the combined method is expected to be acceptable for multidimensional radiative transfer problems with predominant contribution to the source function by emission, especially those problems where hemispherical characteristics are of interest.

Figure 3. Angular variation of the dimensionless radiation flux for problem 1: 1 - combined method; 2 - transport MC, 3 - reference MC at μ = 0.5, and 4 - reference MC at μ = 0.95.
The computational times for the three methods measured on a 2.53 GHz Intel Core 2 Duo processor are summarized in Table 2. The computational time reduction for the transport MC method is 46% and 94% for μ = 0.5 and 0.95, respectively, as compared to the reference method. The combined method is even faster, by more than 1 and 2 orders of magnitude for μ = 0.5 and 0.95, respectively, than the reference method. The computational time savings for both methods become more pronounced with an increasing fraction of forward-scattered radiation. This is explained by the fact that the computational time required by the reference method increases with the increasing value of the asymmetry factor of scattering.
Table 2. Computational time (in s) for the methods studied at τtr0 = 1 and ωtr = 0.5
| Problem | Computational method | |||
| Combined | Transport MC | Reference MC | ||
| μ = 0.5 | μ = 0.95 | |||
| 1 | 88 | 780 | 1443 | 13131 |
| 2 | 88 | 512 | 925 | 8198 |
Problem 2. - The cylindrical medium is nonemitting (cold), but the bottom wall of the cylinder (the wall observed from the cylinder center at μ = -1) is diffusely emitting and perfectly absorbing. The results of calculations for this problem are presented in Fig. 4. One can see that the error of the combined method is significant. These results were anticipated based on the early analysis by Dombrovsky et al. (1991), revealing the large error of the two-step combined method for the searchlight effect. A more detailed numerical study by Dombrovsky and Lipiński (2010) showed that the relative error of the combined method with respect to the transport MC method decreases with the optical thickness, especially for higher values of the scattering albedo (at least in the range of ωtr > 0.5). This result is explained by a smoother angular distribution of the radiative intensity in the case of predominant scattering and higher optical thickness of the medium. The behavior of the combined method can be explained as suggested by Dombrovsky (1996a). The “correction” of the strong (or even stepwise) angular dependence of radiative intensity in the P1 approximation was treated in Dombrovsky’s work (1996a) as an additional fictitious scattering or “scattering by approximation.” As a result, the P1-based results are similar to those obtained for media with more intense scattering. In our case, one can see that the two-step combined method overestimates the scattering in the backward hemisphere and in the directions close to the normal, whereas the remaining radiation into the directions close to the forward hemisphere appears to be considerably underestimated.
Problem 2. - The cylindrical medium is nonemitting (cold), but the bottom wall of the cylinder (the wall observed from the cylinder center at μ = -1) is diffusely emitting and perfectly absorbing. The results of calculations for this problem are presented in Fig. 4. One can see that the error of the combined method is significant. These results were anticipated based on the early analysis by Dombrovsky et al. (1991), revealing the large error of the two-step combined method for the searchlight effect. A more detailed numerical study by Dombrovsky and Lipiński (2010) showed that the relative error of the combined method with respect to the transport MC method decreases with the optical thickness, especially for higher values of the scattering albedo (at least in the range of ωtr > 0.5). This result is explained by a smoother angular distribution of the radiative intensity in the case of predominant scattering and higher optical thickness of the medium. The behavior of the combined method can be explained as suggested by Dombrovsky (1996a). The “correction” of the strong (or even stepwise) angular dependence of radiative intensity in the P1 approximation was treated in Dombrovsky’s work (1996a) as an additional fictitious scattering or “scattering by approximation.” As a result, the P1-based results are similar to those obtained for media with more intense scattering. In our case, one can see that the two-step combined method overestimates the scattering in the backward hemisphere and in the directions close to the normal, whereas the remaining radiation into the directions close to the forward hemisphere appears to be considerably underestimated.
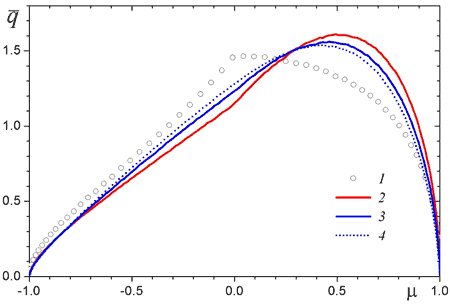
Figure 4. Angular variation of the dimensionless radiation flux for problem 2: 1 - combined method; 2 - transport MC, 3 - reference MC at μ = 0.5, and 4 - reference MC at μ = 0.95.
The variation of the radiation flux with the asymmetry factor of scattering in problem 2 is more pronounced as compared to that in problem 1. Nevertheless, the error of the transport MC method is not large. The directional flux distribution obtained by the transport approximation is physically correct, i.e., the location of the flux maximum, and the flux trends are predicted correctly. In contrast, the results of the combined method are far from the reference solution. Note that the engineering estimates at the realistic values of ωtr ≥ 0.95 and τtrR ≈ 10 for rocket boosters can still be based on the combined two-step method (Dombrovsky, 1996a,b; see also Thermal radiation of two-phase exhaust jet).
In many engineering applications, only the hemispherical characteristics are of interest. A comparison of the computational results shows that both the combined and transport MC methods can provide satisfactory results. It is important that both the transport MC and combined methods enable large reduction in the computational times for both problems. Interestingly, the computational time is practically the same as that problem 1, and the effect of the asymmetry factor of scattering on the computational time of the reference method is very similar for both problems.
Analysis of the results obtained for problems 1 and 2 allows us to conclude that the combined method can be used for radiative transfer problems in scattering media, with medium emission being the dominant source of radiation as compared to the contribution by wall emission and by incident external fluxes. In the case of high optical thickness, the combined method can be employed even for more complicated problems, including those characterized by a considerable contribution of the searchlight effect to the total radiation of the medium.
The combined method becomes more appropriate when hemispherical fluxes (or equivalent directional-hemispherical transmittance and reflectance) are of interest. Examples include inverse radiative transfer analysis for hemispherical flux measurements with isothermal emitting samples. In such studies, properties of the samples are varied in a numerical simulation while repeating the simulations until good agreement between the experimental and numerical data is obtained. Reduction of the computational time in a single simulation will lead to a significant reduction of the overall computational time of the inverse algorithm.
The transport approximation can be used in MC computations for a much wider range of engineering problems, including radiative transfer simulations in anisotropic scattering media such as combustion furnaces, solar thermal receivers and reactors, and other high-temperature applications. It still results in halved computational times as compared to complete MC simulations for moderately forward scattering media.
Propagation of Collimated External Radiation
It was shown in the article Hemispherical transmittance and reflectance at normal incidence that a diffusion approximation (two-flux or P1) can be employed to determine hemispherical reflectance and transmittance of a scattering medium, even in the case of collimated incident radiation [see paper by Dombrovsky et al. (2006) for more details]. The analysis presented in the abovementioned article was concerned with one-dimensional problems typical of laboratory studies of the radiative properties of thin samples [see review by Baillis and Sacadura (2000) for further details]. In some other applied problems, it is also important to consider a two-dimensional axisymmetric problem when the diameter of the normally incident beam is comparable with the thickness of the medium layer. The spectral radiation intensity should be presented as a sum of the diffuse component J and a term that corresponds to the nonscattered external radiation (Modest, 2003):

|
(9) |
where Iλe is the spectral radiation intensity of the incident beam. In the transport approximation, the resulting RTE has the following form:
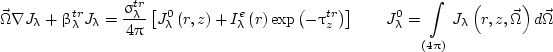
|
(10) |
The presentation of the radiation intensity in the form of Eq. (9) enables one to consider an equivalent problem for the diffuse component of the radiation field. The latter problem can be solved by using the diffusion-based approximate methods.
The applicability of the diffusion approximation to problems of this type was studied by Kolpakov et al. (1990) and by Dombrovsky et al. (1991). The exact solution obtained by Nelson and Satish (1987) for a Gaussian beam is

|
(11) |
Illuminating a plane-parallel layer of a nonabsorbing and isotropic scattering medium was used to estimate the diffusion approximation error. In a more general case, the MC numerical solution obtained by using the computer code by Surzhikov (1987) was used to obtain the benchmark solution. Here we do not reproduce the numerical data of papers (Kolpakov et al., 1990; Dombrovsky et al., 1991) reported in the book by Dombrovsky (1996a); however, the main conclusions obtained in these papers are summarized as follows. The diffusion approximation gives fairly good results for average and large optical distances from the conventional boundary of the beam in the region where the contribution by multiple scattering becomes large. The maximum error in the total radiation intensity computed by using the diffusion approximation is observed in the vicinity of the beam boundary for the optically thin medium layer. The radial profile of the radiation flux at the bottom of the medium layer is accurately predicted by the diffusion (P1) approximation when the layer optical thickness is large. This result is independent of the incident beam diameter. Finally, the computations performed for various scattering phase functions for typical parameters of an erosional plume (the characteristic optical thickness is about unity) show that the transport approximation is fairly accurate for both transmitted and reflected radiation.
REFERENCES
Adzerikho, K. S., Antsulevich, V. I., Lapko, Ya. K., and Nekrasov, V. P., Luminescence of two-phase inhomogeneous media of cylindrical geometry, Int. J. Heat Mass Transfer, vol. 22, no. 1, pp. 131-136, 1979.
Baillis, D. and Sacadura, J.-F., Thermal radiation properties of dispersed media: Theoretical prediction and experimental characterization, J. Quant. Spectrosc. Radiat. Transf., vol. 67, no. 5, pp. 327-363, 2000.
Bobcôo, R. P., Directional emissivities from a two-dimensional, absorbing-scattering medium: The semi-infinite slab, ASME J. Heat Transfer, vol. 89, no. 4, pp. 313-320, 1967.
Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, New York: Begell House, 1996a.
Dombrovsky, L. A., Approximate methods for calculating radiation heat transfer in dispersed systems,Therm. Eng., vol. 43, no. 3, pp. 235-243, 1996b.
Dombrovsky, L. A. and Barkova, L. G., Solving the two-dimensional problem of thermal-radiation transfer in an anisotropically scattering medium using the finite element method, High Temp., vol. 24, no. 4, pp. 585-592, 1986.
Dombrovsky, L. A., Kolpakov, A. V., and Surzhikov, S. T., Transport approximation in calculating the directed-radiation transfer in an anisotropically scattering erosional flare, High Temp., vol. 29, no. 6, pp. 954-960, 1991.
Dombrovsky, L., Randrianalisoa, J., and Baillis, D., Modified two-flux approximation for identification of radiative properties of absorbing and scattering media from directional-hemispherical measurements, J. Opt. Soc. Am. A, vol. 23, no. 1, pp. 91-98, 2006.
Dombrovsky, L. and Lipiński, W., A combined P1 and Monte Carlo model for radiative transfer in multi-dimensional anisotropically scattering media, Proc. of the 14thInt’l. Heat Transfer Conf., Washington, DC, USA, August 8-13, 2010, Paper no. IHTC14-22194.
Edwards, R. N. and Bobcôo, R. P., Radiant heat transfer from isothermal dispersion with isotropic scattering, ASME J. Heat Transfer, vol. 89, no. 4, pp. 300-308, 1967.
Farmer, J. T. and Howell, J. R., Comparison of Monte Carlo strategies for radiative transfer in participating media, Adv. Heat Transfer, vol. 31, pp. 333-429, 1998.
Kolpakov, A. V., Dombrovsky, L. A., and Surzhikov, S. T., Transfer of directed radiation in an absorbing and anisotropically scattering medium, High Temp., vol. 28, no. 5, pp. 753-757, 1990.
Laredo, D. and Netzer, D. W., The dominant effect of alumina on nearfield plume radiation, J. Quant. Spectrosc. Radiat. Transf., vol. 50, no. 5, pp. 511-530, 1993.
Modest, M. F., Radiative Heat Transfer, 2nd ed., New York: Academic Press, 2003.
Nelson, H. F. and Satish, B. V., Transmission of laser beam through anisotropic scattering media, J. Thermophys. Heat Transfer, vol. 1, no. 3, pp. 233-239, 1987.
Ou, S.-Ch. S. and Liou, K.-N., Generalization of the spherical harmonics method to radiative transfer in multi-dimensional space, J. Quant. Spectrosc. Radiat. Transf., vol. 28, no. 4, pp. 271-288, 1982.
Surzhikov, S. T., On directional thermal radiation calculations for light-scattering volumes by use of the Monte Carlo method, High Temp., vol. 25, no. 4, pp. 820-822, 1987.
Surzhikov, S. T., Three-dimensional model of the spectral emissivity of light-scattering exhaust plumes, High Temp., vol. 42, no. 5, pp. 763-775, 2004.
References
- Adzerikho, K. S., Antsulevich, V. I., Lapko, Ya. K., and Nekrasov, V. P., Luminescence of two-phase inhomogeneous media of cylindrical geometry, Int. J. Heat Mass Transfer, vol. 22, no. 1, pp. 131-136, 1979.
- Baillis, D. and Sacadura, J.-F., Thermal radiation properties of dispersed media: Theoretical prediction and experimental characterization, J. Quant. Spectrosc. Radiat. Transf., vol. 67, no. 5, pp. 327-363, 2000.
- Bobcôo, R. P., Directional emissivities from a two-dimensional, absorbing-scattering medium: The semi-infinite slab, ASME J. Heat Transfer, vol. 89, no. 4, pp. 313-320, 1967.
- Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, New York: Begell House, 1996a.
- Dombrovsky, L. A., Approximate methods for calculating radiation heat transfer in dispersed systems,Therm. Eng., vol. 43, no. 3, pp. 235-243, 1996b.
- Dombrovsky, L. A. and Barkova, L. G., Solving the two-dimensional problem of thermal-radiation transfer in an anisotropically scattering medium using the finite element method, High Temp., vol. 24, no. 4, pp. 585-592, 1986.
- Dombrovsky, L. A., Kolpakov, A. V., and Surzhikov, S. T., Transport approximation in calculating the directed-radiation transfer in an anisotropically scattering erosional flare, High Temp., vol. 29, no. 6, pp. 954-960, 1991.
- Dombrovsky, L., Randrianalisoa, J., and Baillis, D., Modified two-flux approximation for identification of radiative properties of absorbing and scattering media from directional-hemispherical measurements, J. Opt. Soc. Am. A, vol. 23, no. 1, pp. 91-98, 2006.
- Dombrovsky, L. and Lipiński, W., A combined P1 and Monte Carlo model for radiative transfer in multi-dimensional anisotropically scattering media, Proc. of the 14thInt’l. Heat Transfer Conf., Washington, DC, USA, August 8-13, 2010, Paper no. IHTC14-22194.
- Edwards, R. N. and Bobcôo, R. P., Radiant heat transfer from isothermal dispersion with isotropic scattering, ASME J. Heat Transfer, vol. 89, no. 4, pp. 300-308, 1967.
- Farmer, J. T. and Howell, J. R., Comparison of Monte Carlo strategies for radiative transfer in participating media, Adv. Heat Transfer, vol. 31, pp. 333-429, 1998.
- Kolpakov, A. V., Dombrovsky, L. A., and Surzhikov, S. T., Transfer of directed radiation in an absorbing and anisotropically scattering medium, High Temp., vol. 28, no. 5, pp. 753-757, 1990.
- Laredo, D. and Netzer, D. W., The dominant effect of alumina on nearfield plume radiation, J. Quant. Spectrosc. Radiat. Transf., vol. 50, no. 5, pp. 511-530, 1993.
- Modest, M. F., Radiative Heat Transfer, 2nd ed., New York: Academic Press, 2003.
- Nelson, H. F. and Satish, B. V., Transmission of laser beam through anisotropic scattering media, J. Thermophys. Heat Transfer, vol. 1, no. 3, pp. 233-239, 1987.
- Ou, S.-Ch. S. and Liou, K.-N., Generalization of the spherical harmonics method to radiative transfer in multi-dimensional space, J. Quant. Spectrosc. Radiat. Transf., vol. 28, no. 4, pp. 271-288, 1982.
- Surzhikov, S. T., On directional thermal radiation calculations for light-scattering volumes by use of the Monte Carlo method, High Temp., vol. 25, no. 4, pp. 820-822, 1987.
- Surzhikov, S. T., Three-dimensional model of the spectral emissivity of light-scattering exhaust plumes, High Temp., vol. 42, no. 5, pp. 763-775, 2004.