Thermal Radiation from a Spherical Particle to an Absorbing Medium Through a Narrow Concentric Gap
Following from: The Mie solution for spherical particles; Thermal radiation from nonisothermal spherical particles
Leading to: Thermal radiation from nonisothermal particles in combined heat transfer problems
The interest to heat transfer by thermal radiation from a spherical particle to an ambient absorbing medium through a narrow concentric gap between the particle and the medium was stimulated by the so-called FCI problem. It is a problem of fuel-coolant interaction in the case of a hypothetical nuclear reactor severe accident. The dynamic and thermal interaction of core melt (corium) with ambient water is accompanied by fragmentation of the melt jet into small droplets. The subsequent heat transfer from the corium droplets to ambient water may lead to a dangerous steam explosion (Corradini et al., 1988; Theofanous, 1995; Berthoud, 2000). Simple estimates show that thermal radiation is an important heat transfer mode due to the very high temperature of the melt (~3000 K) (Dinh et al., 1999; Fletcher, 1999; Dombrovsky, 1999a, 2000a).
Because of the inertia of the liquid, the steam blanket of a hot corium particle is subjected to high-frequency oscillations. This steam blanket may collapse, which leads to a small-scale steam explosion. In so doing, the steam layer thickness at different stages of the process may range from several to hundreds of microns (Kim and Corradini, 1988; Dombrovsky and Zaichik, 2000; Gubaidullin and Sannikov, 2005). Obviously, the radiation flux is less sensitive to the variation of the steam layer thickness than the heat flux due to thermal conductivity of steam. As a result, thermal radiation both affects the average intensity of heat transfer from a particle to liquid and has a damping effect on the oscillation of the steam blanket of the particle. The wide range of variation of the steam layer thickness necessitates the development of a rather general theoretical description of the radiation transfer.
In this article, a theoretical model for calculating the radiation heat flux from a hot particle through the concentric steam layer is presented. According to Dombrovsky (1999a, 2000a), the analysis includes the case of a small thickness of the steam layer Δ, which may be comparable with the radiation wavelength. The physical models being treated and the mathematics employed are fairly general. At the same time, the performed numerical analysis is restricted with respect to the optical properties of the materials, i.e., the interaction between molten oxide particles and water is treated, which is of most interest as regards the safety of light water nuclear reactors. Having in mind that the calculation of the radiation heat transfer is only one part of a general multiphase flow model, special attention is given to approximate computational procedures.
General Wave Solution for Radiation Flux
Let us consider a single spherical particle of radius r0 in a concentric cavity of radius ri. The particle and water in the volume ri < r < ∞ are isothermal, their temperatures are equal to T0 and Te(T0 > Te) correspondingly, and the complex indices of refraction are m = n - iκ and me = ne - iκe. The specific spectral radiation flux on the particle surface is defined as follows:
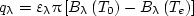
|
(1) |
where function ελ(x,y,m,me) is the spectral emissivity of the system “particle cavity,” and the diffraction parameter of the particle and that of the cavity are usually defined as

|
(2) |
The general solution to the problem under consideration at arbitrary values of parameters has been derived by Levin et al. (1980) by use of the fluctuation-dissipation theorem (Levin and Rytov, 1967). One can also remember some particular solutions reported earlier by Carvalho et al. (1967), Polder and van Hove (1971), and Caren (1974). A similar approach for narrow clearance and layered structures is used in radiation heat transfer calculations in microscale electronics when the wave effects prove very significant (Tien and Chen, 1994; Chen, 1997; Chen, 2005). The microscale radiation heat transfer is a developing branch of the present-day heat transfer theory; it is beyond the scope of this article, and one can read recent book by Zhang (2008) and review by Francoeur and Mengüç (2008) for more details.
For a single spherical particle in a concentric cavity, the analytical solution for the spectral emissivity ελ was derived by Averin (1987, 1991). This solution can be written using the notations of the Mie theory in the following form:

|
(3a) |

|
(3b) |
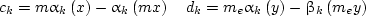
|
(3c) |

|
(3d) |
where

|
(4) |
and ψk,ζk are the Riccati-Bessel functions. Note that in the special case of nonabsorbing medium (κe = 0), the known solution for radiation absorption by a two-layer spherical particle in a vacuum (Bohren and Huffman, 1983; Dombrovsky, 1996) can be used, and the spectral emissivity is calculated as follows:

|
(5) |
where γ = ri/r0 = y/x, Qa is the efficiency factor of absorption for a two-layer particle, which consists of (1) the central core with the diffraction parameter x' = nex and the complex refractive index m' = m/ne and (2) the nonabsorbing concentric layer with the diffraction parameter x'' = ney and the index of refraction n'' = 1/ne. One can see that in the absence of the steam layer between the particle and the water (γ = 1), the value of ελ proves to be ne2 times greater than the value ελ(0) for the same particle in a vacuum.
Particular Cases of Zero or Large Thickness of the Gap
In the case of zero thickness of the steam layer between the particle and ambient water, the problem degenerates to the case when the particle is immersed in an absorbing and refracting medium. This particular problem was discussed in the article Radiative properties of gas bubbles in a semitransparent medium. In the opposite case of a great thickness of the steam layer (in comparison with the wavelength), the particle emissivity does not depend on optical constants of water. Note that in the case of me - 1me = 1, γ = 1, one can derive from the general equation (3a) the relation for spectral emissivity of a single particle ελ(0) (Prishivalko, 1983; Dombrovsky, 1999b, 2000b). The resulting expression coincides with the formula for the efficiency factor of absorption [see Eq. (3) from the article Thermal radiation from nonisothermal spherical particles].
In the case of negligible wave effects, the spectral emissivity of the system particle-water can be calculated by the regular formula

|
(6) |
where ελ(i) is the hemispherical emissivity of the water surface. The latter value is determined using the Fresnel equations for randomly polarized radiation (Born and Wolf, 1999),

|
(7a) |

|
(7b) |
Note that 1 - ελ(i) << 1, and therefore one can use the approximate equality ελ ≈ ελ(0), even for not-so-large values of γ.
From the known value of the spectral radiation flux on the particle surface, one can calculate the radial profile of heat absorption in surrounding water. In so doing, one should bear in mind that radiation intensity in the region r > ri is not isotropic, but the radiation is concentrated in a solid angle, whose magnitude depends on the geometric parameter γ and on the index of refraction ne. Keeping in mind that reflection of the thermal radiation from the vapor-water interface is small, the heat absorption profile may be characterized by the following dimensionless function:

|
(8a) |
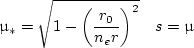
|
(8b) |
and the specific power of absorbed radiation is determined by integration over the spectrum

|
(9) |
Note that the following energy balance equation takes place:

|
(10) |
where q is the integral radiation flux on the particle surface, and it is convenient to use the dimensionless function, which characterizes a part of the integral radiation flux absorbed in spherical water layer (ri,r),

|
(11) |
Following paper by Dombrovsky (2000a), consider some numerical results typical of metal oxide particles in water. We use the spectral optical constants of molten aluminum oxide at temperature T = 3000 K as referenced spectral dependences, but consider two variants of the index of absorption,

|
(12a) |
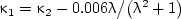
|
(12b) |
where λ is expressed in microns. The numerical data for spectral emissivity of the system “particle concentric cavity” obtained by accounting for wave effects are presented in Figs. 1 and 2 in the form of ελ(δ) dependences, where δ = γ-1 is the relative thickness of the vapor layer.
 |  |
| (a) | (b) |
Figure 1. Spectral emissivity of an oxide particle in a concentric cavity in ambient water at λ = 1 μm and various values of the diffraction parameter x; 1 and 2 are numbers of variants of the oxide absorption index; dots at δ = 0 and horizontal asymptotes, shown for x = 50 and x = 100 are from Mie theory calculations.

Figure 2. Spectral emissivity of oxide particle in a concentric cavity in ambient water at λ = 3 μm: 1 and 2, exact solution with the wave effects (1 and 2 are numbers of variants of the oxide absorption index); 3, approximation (13) based on the Mie solution.
One can see in Fig. 1 that the emissivity, generally speaking, is a complex nonmonotonic function of the vapor layer thickness, although two limiting cases of δ = 0 and δ→∞ are described by the Mie theory. As a rule, the value of ελ increases with the particle radius. This effect is more pronounced for a weakly absorbing oxide (variant 1). For comparably large particles (x ≥ 50), dependencies ελ(δ) are simpler and one can use the following exponential approximation:

|
(13a) |

|
(13b) |
The asymptotic value of ελ = ελ(0) in the limit δ = γ - 1 >> 1/x corresponds to a single particle in a vacuum, whereas the value ελ = ελ(1) when δ = 0 is determined as that for the particle immersed in a reflecting but nonabsorbing medium. One can see in Fig. 2 that the results of calculation by Eq. (13) are in good agreement with the exact solution including the wave effects. More detailed results on spectral behavior of the emissivity as well as some data for radial profiles of radiation power absorbed in water can be found in papers by Dombrovsky (1999a, 2000a).
REFERENCES
Averin, V. V., Radiation Heat Transfer Calculation in Narrow Clearances between a Sphere and Concentric Cavity, Trans. Mosc. Inst. Power Eng., vol. 149, pp. 63-67, 1987 (in Russian).
Averin, V. V., Unique Features of Heat Exchange for Spherical Particles in a Concentric Cavity, J. Eng. Phys. Thermophys., vol. 60, no. 4, pp. 468-472, 1991.
Berthoud, G., Vapor Explosions, Ann. Rev. Fluid Mech., vol. 32, pp. 573-611, 2000.
Bohren, C. F. and Huffman, D. R., Absorption and Scattering of Light by Small Particles, Wiley, Hoboken, NJ, 1983.
Born, M. and Wolf, E., Principles of Optics, 7th (expanded) ed., Cambridge University Press, Cambridge, England, 1999.
Caren, R. P., Thermal Radiation Between Closely Spaced Metal Surfaces at Low Temperature Due to Traveling and Quasi-Stationary Components of the Radiation Field, Int. J. Heat Mass Transfer, vol. 17, no. 7, pp. 755-765, 1974.
Carvalho, E. G., Tien, C. L., and Caren, R. P., Effect of Small Spacing on Radiative Transfer Between Two Dielectrics, ASME J. Heat Transfer, vol. 89, no. 4, pp. 351-357, 1967.
Chen, G., Wave Effects on Radiative Transfer in Absorbing and Emitting Thin-Film Media, Microscale Thermophys. Eng., vol. 1, no. 3, pp. 215-223, 1997.
Chen, R.-L., Radiative Heat Transfer between two Closely-Spaced Plates, AIAA Paper No. 960, 2005.
Corradini, M. L., Kim, B. J., and Oh, M. D., Vapor Explosion in Light Water Reactors: A Review of Theory and Modeling, Prog. Nucl. Energy, vol. 22, no. 1, pp. 1-117, 1988.
Dinh, T. N., Dinh, A. T., Nourgaliev, R. R., and Sehgal, B. R., Investigation of Film Boiling Thermal Hydraulics under FCI Conditions: Results of Analyses and Numerical Study, Nucl. Eng. Des., vol. 189, no. 1-3, pp. 251-272, 1999.
Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
Dombrovsky, L. A., Radiation Heat Transfer from a Spherical Particle via Vapor Shell to the Surrounding Liquid, High Temp., vol. 37, no. 6, pp. 912-919, 1999a.
Dombrovsky, L. A., Thermal Radiation of a Spherical Particle of Semitransparent Material, High Temp., vol. 37, no. 2, pp. 260-269, 1999b.
Dombrovsky, L. A., Radiation Heat Transfer from a Hot Particle to Ambient Water through the Vapor Layer, Int. J. Heat Mass Transfer, vol. 43, no. 13, pp. 2405-2414, 2000a.
Dombrovsky, L. A., Thermal Radiation from Nonisothermal Spherical Particles of a Semitransparent Material, Int. J. Heat Mass Transfer, vol. 43, no. 9, pp. 1661-1672, 2000b.
Dombrovsky, L. A. and Zaichik, L. I., The Dynamics of Vapor Void under Conditions of Thermal Interaction of a Hot Spherical Particle with Ambient Water, High Temp., vol. 38, no. 6, pp. 938-947, 2000.
Fletcher, D. F., Radiation Absorption During Premixing, Nucl. Eng. Des., vol. 189, no. 1-3, pp. 435-440, 1999.
Francoeur, M. and Mengüç, M. P., Role of Fluctuational Electrodynamics in Near-Field Radiative Heat Transfer, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, no. 2, pp. 280-293, 2008.
Gubaidullin, A. A. and Sannikov, I. N., The Dynamics and Heat and Mass Transfer of a Vapor Bubble Containing a Hot Particle, High Temp., vol. 43, no. 6, pp. 922-929, 2005.
Kim, B. and Corradini, M. L., Modeling of Small-Scale Single Droplet Fuel/Coolant Interactions, Nucl. Sci. Eng., vol. 98, pp. 16-28, 1988.
Levin, M. L., Polevoi, V. G., and Rytov, S. M., Theory of Heat Transfer Due to a Fluctuation Electromagnetic Field, J. Exper. Theor. Phys., vol. 79, no. 6, pp. 2087-2103, 1980 (in Russian).
Levin, M. L. and Rytov, S. M., Theory of Equilibrium Thermal Fluctuations in Electrodynamics, Nauka, Moscow, 1967 (in Russian).
Polder, D. and van Hove, M., Theory of Radiative Heat Transfer Between Closely Spaced Bodies, Phys. Rev. B, vol. 4, no. 5, pp. 3303-3314, 1971.
Prishivalko, A. P., Optical and Thermal Fields in Light Scattering Particles, Nauka i Tekhnika, Minsk, 1983 (in Russian).
Theofanous, T. G., The Study of Steam Explosions in Nuclear Systems, Nucl. Eng. Des., vol. 155, no. 1-2, pp. 1-26, 1995.
Tien, C. L. and Chen, G., Challenges in Microscale Radiative and Conductive Heat Transfer, ASME J. Heat Transfer, vol. 116, pp. 799-807, 1994.
Zhang, Z. M., Nano/Microscale Heat Transfer, McGraw-Hill, New York, 2008.
References
- Averin, V. V., Radiation Heat Transfer Calculation in Narrow Clearances between a Sphere and Concentric Cavity, Trans. Mosc. Inst. Power Eng., vol. 149, pp. 63-67, 1987 (in Russian).
- Averin, V. V., Unique Features of Heat Exchange for Spherical Particles in a Concentric Cavity, J. Eng. Phys. Thermophys., vol. 60, no. 4, pp. 468-472, 1991.
- Berthoud, G., Vapor Explosions, Ann. Rev. Fluid Mech., vol. 32, pp. 573-611, 2000.
- Bohren, C. F. and Huffman, D. R., Absorption and Scattering of Light by Small Particles, Wiley, Hoboken, NJ, 1983.
- Born, M. and Wolf, E., Principles of Optics, 7th (expanded) ed., Cambridge University Press, Cambridge, England, 1999.
- Caren, R. P., Thermal Radiation Between Closely Spaced Metal Surfaces at Low Temperature Due to Traveling and Quasi-Stationary Components of the Radiation Field, Int. J. Heat Mass Transfer, vol. 17, no. 7, pp. 755-765, 1974.
- Carvalho, E. G., Tien, C. L., and Caren, R. P., Effect of Small Spacing on Radiative Transfer Between Two Dielectrics, ASME J. Heat Transfer, vol. 89, no. 4, pp. 351-357, 1967.
- Chen, G., Wave Effects on Radiative Transfer in Absorbing and Emitting Thin-Film Media, Microscale Thermophys. Eng., vol. 1, no. 3, pp. 215-223, 1997.
- Chen, R.-L., Radiative Heat Transfer between two Closely-Spaced Plates, AIAA Paper No. 960, 2005.
- Corradini, M. L., Kim, B. J., and Oh, M. D., Vapor Explosion in Light Water Reactors: A Review of Theory and Modeling, Prog. Nucl. Energy, vol. 22, no. 1, pp. 1-117, 1988.
- Dinh, T. N., Dinh, A. T., Nourgaliev, R. R., and Sehgal, B. R., Investigation of Film Boiling Thermal Hydraulics under FCI Conditions: Results of Analyses and Numerical Study, Nucl. Eng. Des., vol. 189, no. 1-3, pp. 251-272, 1999.
- Dombrovsky, L. A., Radiation Heat Transfer in Disperse Systems, Begell House, New York and Redding, CT, 1996.
- Dombrovsky, L. A., Radiation Heat Transfer from a Spherical Particle via Vapor Shell to the Surrounding Liquid, High Temp., vol. 37, no. 6, pp. 912-919, 1999a.
- Dombrovsky, L. A., Thermal Radiation of a Spherical Particle of Semitransparent Material, High Temp., vol. 37, no. 2, pp. 260-269, 1999b.
- Dombrovsky, L. A., Radiation Heat Transfer from a Hot Particle to Ambient Water through the Vapor Layer, Int. J. Heat Mass Transfer, vol. 43, no. 13, pp. 2405-2414, 2000a.
- Dombrovsky, L. A., Thermal Radiation from Nonisothermal Spherical Particles of a Semitransparent Material, Int. J. Heat Mass Transfer, vol. 43, no. 9, pp. 1661-1672, 2000b.
- Dombrovsky, L. A. and Zaichik, L. I., The Dynamics of Vapor Void under Conditions of Thermal Interaction of a Hot Spherical Particle with Ambient Water, High Temp., vol. 38, no. 6, pp. 938-947, 2000.
- Fletcher, D. F., Radiation Absorption During Premixing, Nucl. Eng. Des., vol. 189, no. 1-3, pp. 435-440, 1999.
- Francoeur, M. and Mengüç, M. P., Role of Fluctuational Electrodynamics in Near-Field Radiative Heat Transfer, J. Quant. Spectrosc. Radiat. Transfer, vol. 109, no. 2, pp. 280-293, 2008.
- Gubaidullin, A. A. and Sannikov, I. N., The Dynamics and Heat and Mass Transfer of a Vapor Bubble Containing a Hot Particle, High Temp., vol. 43, no. 6, pp. 922-929, 2005.
- Kim, B. and Corradini, M. L., Modeling of Small-Scale Single Droplet Fuel/Coolant Interactions, Nucl. Sci. Eng., vol. 98, pp. 16-28, 1988.
- Levin, M. L., Polevoi, V. G., and Rytov, S. M., Theory of Heat Transfer Due to a Fluctuation Electromagnetic Field, J. Exper. Theor. Phys., vol. 79, no. 6, pp. 2087-2103, 1980 (in Russian).
- Levin, M. L. and Rytov, S. M., Theory of Equilibrium Thermal Fluctuations in Electrodynamics, Nauka, Moscow, 1967 (in Russian).
- Polder, D. and van Hove, M., Theory of Radiative Heat Transfer Between Closely Spaced Bodies, Phys. Rev. B, vol. 4, no. 5, pp. 3303-3314, 1971.
- Prishivalko, A. P., Optical and Thermal Fields in Light Scattering Particles, Nauka i Tekhnika, Minsk, 1983 (in Russian).
- Theofanous, T. G., The Study of Steam Explosions in Nuclear Systems, Nucl. Eng. Des., vol. 155, no. 1-2, pp. 1-26, 1995.
- Tien, C. L. and Chen, G., Challenges in Microscale Radiative and Conductive Heat Transfer, ASME J. Heat Transfer, vol. 116, pp. 799-807, 1994.
- Zhang, Z. M., Nano/Microscale Heat Transfer, McGraw-Hill, New York, 2008.