An error function is defined by the integral
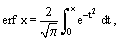
and it occurs frequently in engineering problems; e.g., in heat conduction problems. The error function represents the area under the Gaussian function 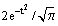 from t = 0 to t = x, so that erf ∞ = 1. The complementary error function is:
from t = 0 to t = x, so that erf ∞ = 1. The complementary error function is:
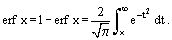
The error function erf x is a monotonically increasing odd function of x; i.e., erf (–x) = –erf x and erf x1 ≤ erf x2 whenever x1 ≤ x2. Its Maclaurin series (for small x) is given by:

and for large values of x, the asymptotic expansion is:
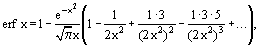
where erf x may be approximated as

There exist extensive tabulations of erf x [see Abramowitz and Stegun (1965), for example].
REFERENCES
Abramowitz, M. and Stegun, I. (1965) Handbook of Mathematical Functions, Dover Publications, New York.
References
- Abramowitz, M. and Stegun, I. (1965) Handbook of Mathematical Functions, Dover Publications, New York. DOI: 10.1119/1.1972842