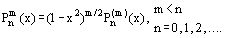LEGENDRE TYPE POLYNOMIALS

Legendre type polynomials or spherical polynomials are polynomials orthogonal on the interval [−1, 1] with unit weight.

Legendre polynomials are defined by:

(1)

The representation

(2)

is valid for Legendre polynomials.

Legendre polynomials are bounded on the interval [−1, 1] by the solution of the differential Legendre equation

(3)

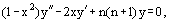
which appears in problems of heat conduction when solving the Laplace equation in spherical coordinates by the separation of variables method.

The following recurrent relations are valid for Legendre polynomials

(4)

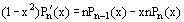
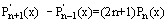
Legendre polynomials have n different real roots. They all lie on the interval [−1, 1]. For Legendre polynomials the representation

(5)

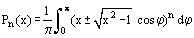
are valid.

Also expressed in terms of Legendre polynomials are adjoint functions, which are often used in soving problems of radiation heat transfer

(6)