Archimedes number Ar is the similarity criterion of two thermal or hydrodynamic phenomena, in which determining factors are the buoyant (Archimedes) force and the viscosity force. Thus
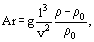
where l is the characteristic linear dimension, ν is the kinematic viscosity, ρ and ρ0 are the medium densities at two points and g is the acceleration due to gravity.
If the variation of the density is caused by a change of temperature T, then at small temperature drops (ρ − ρ)0/ρ0 = βΔT (where β is the volumetric expansion coefficient), the Archimedes number becomes the Grashof Number Gr.
By comparing the volume (mass) forces and the kinetic energy of a moving free-convective flow, we may obtain an estimate of the characteristic velocity of motion
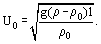
The Archimedes number may then also be represented in the form
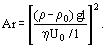
It is possible to consider this expression as ratio of the square of the volume (buoyant) forces to the viscous friction forces.
The molecular friction forces prevent the development of disturbances. The volumetric forces, on the other hand, intensify the disorder of the motion. Therefore, viscous friction and volume forces exert the opposite effect on the liquid flow. For small values of Ar the motion may be laminar, but with increasing Ar the stability of this motion decreases. At a certain critical value of Arc the laminar motion turns into the turbulent one.
Ar is sometimes also characterized as a ratio of the lift force to internal friction force, however, its numerical value in this case is different at different points of the flow.