The Gaussian quadrature method is an approximate method of calculation of a certain integral  . By replacing the variables x = (b – a)t/2 + (a + b)t/2, f(t) = (b – a)y(x)/2 the desired integral is reduced to the form
. By replacing the variables x = (b – a)t/2 + (a + b)t/2, f(t) = (b – a)y(x)/2 the desired integral is reduced to the form  .
.
The Gaussian quadrature formula is

The cusps ti of the Gaussian quadrature formula are the roots of a Legendre polynomial of degree n, Pn(t). The Legendre polynomial has exactly n real and various roots in the interval (–1, 1). The weights Ai of the Gaussian quadrature formula are defined by

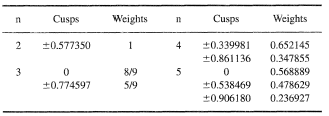
Given in the table are the cusps and weights of the Gaussian quadrature formula for the first five values n.
Gaussian quadrature formula is exact for an arbitrary polynomial of degree not higher than 2n – 1. The remainder term of Gauss' formula Rn for the integral  is expressed as follows
is expressed as follows

The Gaussian quadrature method is applied when a subintegral function is smooth enough and a gain in the number of cusps is essential (for instance, in calculating multiple integrals as iterated integrals).
The Gaussian quadrature formula is widely used in solving problems of radiation heat transfer in direct integration of the equation of transfer of radiation over space. The application of Gauss' formula in this case works very well especially when the number of intervals of spectrum decomposition is great.