Most slurries, suspensions, dispersions, solutions of polymeric materials and melts exhibit complex flow behavior which cannot be described by Newton's law of viscosity τ = ηγ, where τ is the shear stress, γ is the shear rate and the constant of proportionality η is the material property called Viscosity. Convective heat transfer to such fluids depends on the fluid rheology, geometric configuration of the flow domain as well as the flow regime (e.g., laminar, turbulent, etc). The apparent viscosity of Non-Newtonian Fluids, ηa = τ/γ, is not a material property (as is the case for Newtonian Fluids) but may depend on the rate of shear and previous flow history of the fluid. Viscoelastic fluids display properties of both fluids and elastic solids. The following chart presents a rheological classification of non-Newtonian fluids encountered in the chemical, food, petrochemical, detergent, printing inks, coatings, etc. industries.
Convective heat transfer to such fluids depends on the rheology of the fluid. It is affected by viscous dissipation due to the very high viscosities coupled with high shear rates, and the temperature-dependence of the apparent viscosity as well as by thermal conductivity, possible chemical reactions, etc. Due to space limitations, we confine our attention to steady convective heat transfer to pseudoplastic or dilatant fluids described by the well known Ostwald-de-Waele power law model (τ = Kγn or ηa = Kγn−1; n < 1 for pseudoplastic fluids and n > 1 for dilatant fluids). Further, we will examine only internal flow through smooth, straight conduits of circular and noncircular cross-section. Since most non-Newtonian fluids are highly viscous, laminar flow is often encountered in industrial applications. External flows involving non-Newtonian fluids are generally of less practical interest than internal flows. Time-dependent fluids which undergo significant shearing before entry into the channel or duct are affected by the time-dependency only over short times of deformation. Also, except in the hydrodynamically developing entrance region of the duct or channel fluid elasticity has little influence on the flow since the elastic stresses do not change in the flow direction.
Since most non-Newtonian fluids have high viscosities, the hydrodynamic entrance length beyond which the flow becomes independent of axial distance is shorter than the thermal entrance length. Therefore we focus on the case of fully developed velocity profiles, considering a number of geometric configurations, e.g., circular pipe, parallel plates, rectangular ducts, cylindrical annuli and several non-circular cross section ducts. We further restrict attention to rectilinear ducts of uniform cross-section. Effects of viscous dissipation, variable apparent viscosity, effect of buoyancy, chemical reactions, external flow, turbulence, etc. have been discussed in the literature, e.g., Mashelkar (1988), Lawal and Mujumdar (1989), and Etemad and Mujumdar (1994), among others. The interested reader is referred to the excellent textbook by Skelland (1967) for a thorough analysis of non-Newtonian flow and heat transfer.
Since many non-Newtonian fluids can be adequately considered as purely viscous over flow ranges of interest, for the sake of convenience (and with some loss of generality) the correlations and analytical as well as numerical results presented here assume a power law model. For visoelastic fluids elastic effects become of significance only when secondary flows appear in the flow domain. Thus, for a fully developed laminar tube flow there is no mechanism whereby elasticity can play a role. However for rectangular ducts the secondary flows caused by normal stress differences acting on the fluid boundaries cause enhanced heat transfer due to elasticity effects. The convective heat transfer coefficient expressed as the local Nusselt Number, Nux, depends on the duct geometry and the thermal boundary condition applied. The two most commonly used thermal boundary conditions are:
Uniform temperature (T boundary condition),
Uniform heat flux condition (often referred to as H2 boundary condition to denote uniformity in axial as well as peripheral directions).
Further, the flow may be hydrodynamically and thermally developing in the streamwise direction. For a hydrodynamically developed flow the local Nusselt Number in the thermal entrance region can be obtained analytically using the following relations: for Gz > 25p

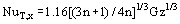
for Gz > 33π, where Graetz Number, Gz, is defined as

For laminar flow through rectangular ducts the Nusselt number is a function of the aspect ratio as well as n. For a fixed aspect ratio the influence of n is less than 10 per cent over 0.5 ≤ n ≤ 1.0 which covers most fluids of practical interest.
The variation of the local Nusselt number with axial distance for a simultaneously developing flow of a power law fluid with Re = 500 and Pr = 10 though a circular tube is shown in Figure 1a and 1b. Both Re and Pr are based on the apparent viscosity of the fluid. Figure 1a shows the variation of NuT,x with dimensionless axial distance Xth for uniform wall temperature for three values of n, viz., n = 0.5 (pseudoplastic), 1.0 (Newtonian) and 1.25 (dilatant). The effect of n on the fully-developed value can be seen to be minimal. Figure 1b shows the corresponding Nusselt number distributions for the H2 thermal boundary condition. The Nusselt numbers are higher for the uniform heat flux boundary condition.
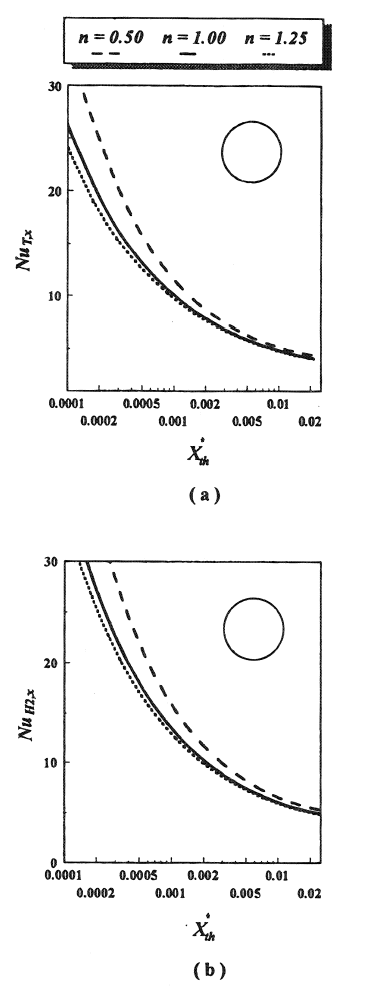
Figure 1. Simultaneously developing flow and heat transfer for Re = 500, Pr = 10. a) Isothermal wall, (2) Constant heat flux wall.
Figure 2a and 2b presents computed Nusselt number distributions for a square duct. Although numerically different (but of the same order) the results display trends similar to those obtained for a circular tube (Figure 1a and 1b). These results were computed by solving the equations of continuity, momentum and energy over the domain of interest. Note that the Nusselt number is dependant on the Prandtl number as well, which is not a fluid property for non-Newtonian fluids unlike Newtonian fluids.
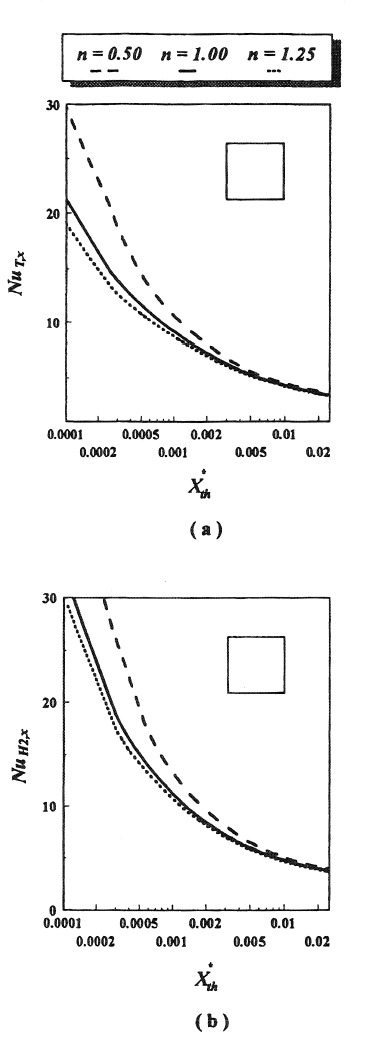
Figure 2. Simultaneously developing flow and heat transfer in square duct for Re = 500 and Pr = 10. (a) Isothermal wall, (b) Constant heat flux at wall.
Table 1 below compares the fully-developed Nusselt numbers (NuT and NuH2) for twelve different cross-sectional geometries. For noncircular ducts the Reynolds number is based on the hydraulic diameter of the duct cross-section. These results were obtained by Etemad (1995) by a finite element solution of the governing conservation equations for Re = 500 and Pr = 10. It is interesting to note the influence of rounding the corners of a square duct; for example, rounding the square duct with a radius one-sixth the side of the duct results in an increase of NuT from 3.19 to 3.43 for n = 0.5. Heat transfer and pressure drop results for power law fluids flowing in various noncircular ducts, including effects of temperature-dependent viscosity as well as viscous dissipation are available in Etemad (1995). A discussion of these aspects is beyond the scope of this text.
Several empirical correlations are available to estimate the fully developed Nusselt number. One may use the following correlations due to Gnielinski for constant temperature as well as constant flux conditions under turbulent flow conditions [Hartnett (1994)]:

where the friction factor f is estimated by

for both round and rectangular ducts. Here

For circular tube, a = 0.25 and b = 0.75. For rectangular ducts, the values of a and b are given below in Table 2 [Hartnett (1994)]. The estimates are within ±20% of measured data. No general correlations exist for heat transfer in turbulent flow of a non-Newtonian fluid. For the flow of dilute suspensions of fibers in water in circular tubes substantial reductions in turbulent flow heat transfer have been reported in the literature at Reynolds numbers up to 2 × 104. However, above this value the heat transfer rate begins to rise sharply.
Relatively little literature exists on predictive correlations useful for engineering design involving non-Newtonian fluids. For space limitations no information is included on external flow heat transfer, viz., flow over objects of various shapes. Also excluded is discussion of such important effects as temperature or composition dependent apparent viscosity, viscous dissipation, viscoelasticity, mixed convection, etc. The reader is referred to the extensive reviews by Metzner (1965), Shenoy and Mashelkar (1982), Lawal and Mujumdar (1989) and Etemad (1995), among others. The textbook by Skelland (1967) is strongly recommended for a tutorial review of the subject matter.
a geometric constant in Kozicki generalized Reynolds number
A area of duct cross-section
b geometric constant in Kozicki generalized Reynolds number
cp Specific heat of fluid
Dh hydraulic diameter 4A/P
f Fanning friction factor
Gz Graetz number
 cp/λx
cp/λx
 mass flow rate
mass flow rate
n power law index
Nux axially local Nusselt number
NuT,x axially local Nusselt number for T boundary condition
NuH2,x axially local Nusselt number for H2 boundary condition
P perimeter of the duct cross-section
Pr Prandtl number η cp(ue/Dh)n−1
Re Reynolds number

Rej Reynolds number ρUDh/(a + b)η
ue inlet velocity
x axial distance
Xth x/Dh Pr·Re
η viscosity of Newtonian fluid
ηa apparent viscosity of non-Newtonian fluid
τ shear stress
γ shear rate (velocity gradient for one-dimensional flow)
ρ density of fluid
λ thermal conductivity of fluid
The author is grateful to Dr. S. Gh. Etemad for his valuable help in the preparation of this contribution.
REFERENCES
Cho, Y. I. and Hartnett, J. P. (1987) Non-Newtonian fluids, Chapter 2 in Handbook of Heat Transfer Applications, 2nd edn. (Ed. Rohsenow, Hartnett, J. P. and Ganic), Kingsport Press.
Etemad, S. Gh., Mujumdar, A. S., Huang, B., (1994) Viscous dissipation effects in entrance region heat transfer for a power law fluid flowing between parallel plates. International Journal of Heat and Fluid Flow, vol. 15, no. 2, 122-131.
Etatnad, S. Gh., Mujumdar, A. S., Huang, B. (1994) Laminar forced convection heat transfer of a non-Newtonian fluid in the entrance region of a square duct with different boundary conditions, 10th International Heat Transfer Conference, Brighton, U.K.
Etemad, S. Gh. (1995) Ph.D. Thesis, McGill University, Montreal, Quebec, Canada.
Hartnett, J. P. (1994) Single phase channel flow forced convection heat transfer, Keynote Lecture, 10th International Heat Transfer Conference, Brighton, U.K.
Irvine, T. F. and Karni, J. (1987) Non-Newtonian fluid flow and heat transfer, Chapter 20 in Handbook of Single Phase Convective Heat Transfer (Ed. Kakac, S., Shah, R. K., Aung, W.), 20-1-20-57.
Lawal, A. and Mujumdar, A. S. (1989) Laminar duct flow and heat transfer to purely viscous non-Newtonian fluids, Advances in Transport Processes, vol. VII (Ed. A. S. Mujumdar and R. A. Mashelkar). Wiley, New York, 353-442.
Mashelkar, M. A. (1988) Convective heat transfer in laminar internal flows design considerations for heat exchanges handling non-Newtonian fluids, Heat Transfer Equipment Design (Ed. R. K. Shah, E. C. Subbarao and R. A. Mashelkar). Hemisphere Publishing Corporation, N.Y. 719-746.
Metzner, A. B. (1965) Heat transfer to non-Newtonian fluids. Advances in Heat Transfer, vol. 2, (Ed. Hartnett, J. P. and Irvine, T. F.) Academic Press, New York, p 357-397.
Shenoy, A. V. and Mashelkar, R. A. (1982) Thermal convection in non-Newtonian fluids, Advances in Heat Transfer, vol. 15, Academic Press, N.Y., 143-225.
Skelland, A. H. P. (1967) Non-Newtonian Flow and Heat Transfer, John Wiley & Sons, New York.
Les références
- Cho, Y. I. and Hartnett, J. P. (1987) Non-Newtonian fluids, Chapter 2 in Handbook of Heat Transfer Applications, 2nd edn. (Ed. Rohsenow, Hartnett, J. P. and Ganic), Kingsport Press.
- Etemad, S. Gh., Mujumdar, A. S., Huang, B., (1994) Viscous dissipation effects in entrance region heat transfer for a power law fluid flowing between parallel plates. International Journal of Heat and Fluid Flow, vol. 15, no. 2, 122-131.
- Etatnad, S. Gh., Mujumdar, A. S., Huang, B. (1994) Laminar forced convection heat transfer of a non-Newtonian fluid in the entrance region of a square duct with different boundary conditions, 10th International Heat Transfer Conference, Brighton, U.K.
- Etemad, S. Gh. (1995) Ph.D. Thesis, McGill University, Montreal, Quebec, Canada.
- Hartnett, J. P. (1994) Single phase channel flow forced convection heat transfer, Keynote Lecture, 10th International Heat Transfer Conference, Brighton, U.K.
- Irvine, T. F. and Karni, J. (1987) Non-Newtonian fluid flow and heat transfer, Chapter 20 in Handbook of Single Phase Convective Heat Transfer (Ed. Kakac, S., Shah, R. K., Aung, W.), 20-1-20-57.
- Lawal, A. and Mujumdar, A. S. (1989) Laminar duct flow and heat transfer to purely viscous non-Newtonian fluids, Advances in Transport Processes, vol. VII (Ed. A. S. Mujumdar and R. A. Mashelkar). Wiley, New York, 353-442.
- Mashelkar, M. A. (1988) Convective heat transfer in laminar internal flows design considerations for heat exchanges handling non-Newtonian fluids, Heat Transfer Equipment Design (Ed. R. K. Shah, E. C. Subbarao and R. A. Mashelkar). Hemisphere Publishing Corporation, N.Y. 719-746.
- Metzner, A. B. (1965) Heat transfer to non-Newtonian fluids. Advances in Heat Transfer, vol. 2, (Ed. Hartnett, J. P. and Irvine, T. F.) Academic Press, New York, p 357-397.
- Shenoy, A. V. and Mashelkar, R. A. (1982) Thermal convection in non-Newtonian fluids, Advances in Heat Transfer, vol. 15, Academic Press, N.Y., 143-225.
- Skelland, A. H. P. (1967) Non-Newtonian Flow and Heat Transfer, John Wiley & Sons, New York.

